SICP学习笔记和习题解答
这里记录了我在学习SICP的过程中的一点笔记,以及作业解答,现在还正在学习中。。(因为作业太多了,读起来真慢。。)
构造过程抽象
求值模型
- 正则序求值:先将复合式代入实际参数,再逐渐展开,直到得到一个只包含基本运算符的表达式,再对其进行求值。(完全展开而后归约)
- 应用序求值:对于复合型表达式,将能进行计算的一些子表达式求值,再对其进行展开,再求值能够进行计算的子表达式,直到求出最终结果。(展开一层归约一层)
练习1.2
(/ (+ 5 4 (- 2 (- 3 (+ 6 (/ 4 5))))) (* 3 (- 6 2) (- 2 7)))
练习1.3
;; the answer below is wrong!!!
(define (sum-of-max-two a b c)
(cond ((< a b) (if (< a c) (+ b c) (+ a b)))
(else (if (< b c) (+ a c) (+ a b)))))
练习1.5
初看到 (define (p) (p)) 这样的定义吓了我一跳,细看其实是一个递归函数的定义,但由没有退出条件,所以一旦有 (p) 这样的调用,程序将陷入死循环。
再看 (test 0 (p)) ,如果是正则序,那么会完全展开再求值,于是会有如下过程:
1. (if (= 0 0) 0 (p)) 2. (if #t 0 (p)) 3. return value, 0
如果是应用序,则会先求值 (p) ,于是程序陷入死循环。
练习1.6
这个题目看了半天,大概猜到是跟求值模型相关的,但在解释器racket上试,和使用原始版本的if结果一模一样。。
于是,无奈Google之,发现此帖,讲得很详细,看来对求值模型还是理解不够,但关键是,racket解释器在实验练习1.5时明明是陷入死循环了,说明是应用序才对,但这里又工作得好好的,真让人搞不懂。。
练习1.7
另一个 good-enough? 函数:
(define (good-enough? guess x) (< (/ (abs (- (improve guess x) guess)) guess) 0.00001))
这个函数不是用绝对误差来作比较,而是用两次guess的变化率来比较,这在处理很小的数时会比较有用,比方说小数0.0000000001这种,但在处理大数时,反而会增加误差,因为计算变化率的分母很大,导致分子很大时依然能满足要求,所以在处理大数时不如先前版本的绝对误差精确。
练习1.8
牛顿法解立方根:
(define (3sqrt guess x)
(if (good-enough? guess x)
guess
(3sqrt (improve guess x) x)))
(define (improve guess x)
(/ (+ (/ x (* guess guess)) (* 2 guess)) 3))
(define (good-enough? guess x)
(< (/ (abs (- (improve guess x) guess)) guess) 0.00001))
线性递归和迭代
作为一个递归过程,但其计算过程可能会是递归的,也可能是迭代的。以阶乘计算为例:
;; 第一种定义
(define (factorial n)
(if (= n 1)
1
(* n (factorial (- n 1)))))
;; 第二种定义
(define (factorial n)
(define (fact-iter result counter)
(if (> counter n)
result
(fact-iter (* result counter) (+ counter 1))))
(fact-iter 1 1))
毫无疑问两种定义都使用了递归过程,但两者有些不同:第一种在计算时会导致 factorial 自身的展开,而且用于计算的n越大,展开的层数越多;第二种在计算时,只需要维护 result 以及 counter 两个变量即可。
在上面的例子中,第一种定义就是递归计算过程,第二种则是迭代计算过程。由于两者都是线性的,所以都是线性过程。(所谓线性是指,第一种的展开长度对于n是线性增长的;第二种的计算步骤对于n是线性增长的)
练习1.9
这是一个递归计算过程:
(inc (+ 3 5)) (inc (inc (+ 2 5))) (inc (inc (inc (+ 1 5)))) (inc (inc (inc (inc (+ 0 5))))) (inc (inc (inc (inc 5)))) (inc (inc (inc 6))) (inc (inc 7)) (inc 8) 9
这是一个迭代计算过程:
(+ 3 6) (+ 2 7) (+ 1 8) (+ 0 9) 9
练习1.10
(A 1 10) => 1024 (A 2 4) => 65536 (A 3 3) => 65536
f(n) = 2n g(n) = 2^n h(n) = 2^h(n-1)
练习1.11
n < 3, f(n) = n; n >= 3, f(n) = f(n-1) + 2f(n-2) + 3f(n-3)
递归过程:
(define (f n)
(cond ((< n 3) n)
(else (+ (f (- n 1))
(* 2 (f (- n 2)))
(* 3 (f (- n 3)))))))
迭代过程:
a = f(2) = 2, b = f(1) = 1, c = f(0) = 0 a <= a + 2b + 3c b <= a c <= b
(define (f2 n)
(f2-iter 2 1 0 n))
(define (f2-iter a b c count)
(if (= count 0)
c
(f2-iter (+ a (* 2 b) (* 3 c)) a b (- count 1))))
练习1.12
杨辉三角的规律:f(n, 1) = f(n, n) = 1, f(n, m) = f(n-1, m-1) + f(n-1, m), 1 < m < n
(define (pascal-triangle n m)
(if (or (= m 1) (= m n))
1
(+ (pascal-triangle (- n 1) (- m 1))
(pascal-triangle (- n 1) m))))
练习1.13
暂时跳过,现在手头只有一台电脑,草稿纸和笔都没有,无法证明。。
整个计算过程涉及到一些数学符号,如果只用文本格式写会很蛋疼,于是,只写个思路:
- 按提示,证明
Fib(n) = (φ^n - ψ^n) / √5,其中φ = (1 + √5) / 2,ψ = (1 - √5) / 2,证明过程比较简单,根据数学归纳法和Fib(n)的定义即可。 - 之后,要证明Fib(n)是最接近φ^n/√5的整数,只需要证明
|Fib(n) - φ^n/√5| ≤ 0.5即可。经过化简,需要证明的不等式变成|ψ^n / √5| ≤ 0.5。 经过观察,
|ψ^n / √5|实际上是趋于0的极限,所以只需要证明两点即可:|ψ^n / √5| ≤ |ψ^(n-1) / √5||ψ^0 / √5| ≤ 0.5
这两点都是比较好证明的。于是再反推回到第二步,就证明了Fib(n)是离φ^n/√5最近的整数。
练习1.14
再略过。。手头没有笔和纸,泪流满面。。
练习1.15
a) 这个问题一时半会儿不知道如何作答,就直接暴力地在函数 p(x) 的定义中加了一个打印函数来打印x以确定被调用了几次,结果显示, (sine 12.15) 调用了5次 p(x) 函数。
b) 对 (sine a) 进行展开,第一次后a变成a/3,第二次变成a/9,所以,在n次之后,a变成了a除以3的n次方。空间和步数是正比于展开次数n的,所以,n关于a的阶就是空间和步数关于a的阶。展开的终止条件是 a / 3^n ≤ 0.1 ,可以求出 n ≥ log3(10a) ,即n会大于等于以3为底10a的对数。所以空间和步数关于a的增长阶是对数的。
练习1.16
题目要求:1.只能用迭代,不能递归;2.增长的阶是对数级。
被这个题的提示给坑到了。。因为提示说维持一个附加变量a来保存计算值,于是我就按提示构造了一个状态变量a,打算用来保存每次迭代的计算值,但经过演算发现必须在第一步迭代将a从1直接给过渡到b^(n/2),不然后面的迭代没法继续,但这肯定是不可能的。。
无奈,去网上搜了一下,当我看到下面这两个等式的时候,我瞬间就明白了:
- n为偶数时:a(b^2)^(n/2) = ab^n
- n为奇数时:ab*b^(n-1) = ab^n
按上面的等式写出迭代过程:
n为偶数时: a <= a b <= b^2 n <= n / 2 n为奇数时: a <= a * b b <= b n <= n - 1
于是,解答如下:
(define (fast-expt b n)
(fast-expt-iter 1 b n))
(define (fast-expt-iter a b n)
(cond ((= n 0) a)
((even? n) (fast-expt-iter a (* b b) (/ n 2)))
(else (fast-expt-iter (* a b) b (- n 1)))))
(define (even? n)
(= (remainder n 2) 0))
这明明是a和b共同保存中间值,以2^10为例,10 => 5 => 4 => 2 => 1 => 0,大多时候a都在打酱油,而b才是保存中间值的主力。。
练习1.17
(define (my* a b)
(cond ((= b 0) 0)
((even? b) (my* (double a) (halve b)))
(else (+ a (my* a (- b 1))))))
(define (double a)
(+ a a))
(define (halve a)
(/ a 2))
练习1.18
有了1.16的基础,再来这道题就好多了,这题的难点是构造类似1.16中的ab^n。和1.16不同,这里的构造等式如下(状态变量定义为s):
- b为偶数:s + ab = s + a*2 * b/2
- b为奇数:s + ab = (s + a) + a * (b - 1)
于是,有如下解:
(define (my* a b)
(my*-iter 0 a b))
(define (my*-iter s a b)
(cond ((= b 0) s)
((even? b) (my*-iter s (double a) (halve b)))
(else (my*-iter (+ s a) a (- b 1)))))
练习1.19
这个题是要求p'和q',根据T^2 = T',可以得到两个关于p'和q'的方程,联立方程可得解。
这两个二元一次方程本身不难,但因为项太多,还有平方,所以如果打字打出来会很蛋疼,所以就不打了,最后解出的结果是:
p' = p^2 + q^2 q' = q^2 + 2pq
吐槽:外国人真尼玛牛,一个特例斐波那契数列,能想到通用的T变换,而且,还尼玛T^2 = T'。。
练习1.20
个人觉得这个题的水平略低,因为只是按照定义对过程调用进行展开而已。关键是,如果你展开的内容少一点也可以接受,但是 (gcd 206 40) 的正规序展开内容太多了,我写了几层,就写不下去了。。最后看了这里的详细展开内容,那哥们真是耐得住。。其实题目的意思大概是想让我们对这两种展开方式有一个比较深刻的理解,但这样大量的重复性工作,显得没有必要,所以我没有耐得住寂寞展开到最后。。从那哥们展开的结果来看,最后的答案是18和4。
练习1.21
把书中的的 smallest-divisor 及相关定义照执行一遍就行了,结果如下:
(smallest-divisor 199) => 199 (smallest-divisor 1999) => 1999 (smallest-divisor 19999) => 7
PS:SICP中文翻译中错误很多啊,比方说上面跟 smallest-divisor 相关的 divides? 定义,其中对 remainder 过程的调用就把参数a和b写反了,坑爹。。页脚的注释d/n应该是n/d。。
练习1.22
我使用的Scheme实现是Racket,这个实现并没有包含如题目中所说的 runtime ,于是我Google了一下,发现有一个过程叫 current-inexact-milliseconds 可以达到要求,于是就用它代替了 runtime 。
这个题目的实现代码如下:
(define (timed-prime-test n)
(newline)
(display n)
(start-prime-test n (current-inexact-milliseconds)))
(define (start-prime-test n start-time)
(if (prime? n)
(report-time (- (current-inexact-milliseconds) start-time))
#f)) ;; 这里因为Racket实现不允许if只有一个分支,所以用#f来表示另一个分支
(define (report-time elapsed-time)
(display " *** ")
(display elapsed-time))
(define (search-for-primes start count)
(cond ((= count 0) (newline))
((timed-prime-test start) (search-for-primes (next-odd start) (- count 1)))
(else (search-for-primes (next-odd start) count))))
(define (next-odd n)
(if (= (remainder n 2) 0)
(+ 1 n)
(+ 2 n)))
测试了几组数据,得到以下结果(不是奇数的行已删去):
100000000003 *** 24.06689453125 100000000019 *** 14.223876953125 100000000057 *** 15.403076171875 > 1000000000039 *** 49.025146484375 1000000000061 *** 48.720947265625 1000000000063 *** 47.57080078125 > 10000000000037 *** 154.43701171875 10000000000051 *** 143.823974609375 10000000000099 *** 147.25390625
取平均值除了一下,时间比值为2.706和3.066,这两个离√10还差得比较多,不过可能是受CPU,系统环境的影响,随机性较强,不过比值应该是√10这一点还是很明确的。
练习1.23
(define (next n)
(if (= n 2)
3
(+ n 2)))
(define (find-divisor n test)
(cond ((> (* test test) n) n)
((divides? n test) test)
(else (find-divisor n (next test)))))
得到结果如下(取了三组和1.22中对应的值):
100000000003 *** 14.049072265625 100000000019 *** 10.261962890625 100000000057 *** 9.14697265625 > 1000000000039 *** 40.97705078125 1000000000061 *** 30.837890625 1000000000063 *** 31.4189453125 > 10000000000037 *** 103.964111328125 10000000000051 *** 102.067138671875 10000000000099 *** 94.930908203125
分别计算平均消耗时间比值,得到三个值:1.61,1.41,1.48,这几个值是明显是小于2的。可能虽然步数是少了一半,但是在运行过程中的一些其它消耗,导致了时间比值小于2。
然后我又试了一下,证明这多出来的时间消耗是来自 next 过程调用,将 find-divisor 以及 smallest-divisor 过程进行重定义为以下形式:
(define (find-divisor n test)
(cond ((> (* test test) n) n)
((divides? n test) test)
(else (find-divisor n (+ test 2))))) ;; 直接加2,不再调用next过程
(define (smallest-divisor n)
(find-divisor n 3)) ;; 直接从3开始
结果如下:
100000000003 *** 13.234130859375 100000000019 *** 8.0458984375 100000000057 *** 7.89599609375 > 1000000000039 *** 28.672119140625 1000000000061 *** 25.3388671875 1000000000063 *** 25.071044921875 > 10000000000037 *** 78.4560546875 10000000000051 *** 78.115966796875 10000000000099 *** 71.85498046875
可以看到,这里的时间消耗确实是比1.22中减半了。
练习1.24
这个练习,将 start-prime-test 中的 prime? 换成 fast-prime? 即可:
(define (start-prime-test n start-time)
(if (fast-prime? n 3) ;; 测试的次数取3
(report-time (- (current-inexact-milliseconds) start-time))
#f))
然后进行测试,得到以下结果(最高只能到10的9次方,因为再高的话,超过了int型的最大值,这时 random 函数会报错):
1009 *** 0.014892578125 1013 *** 0.01611328125 1019 *** 0.015869140625 > 10007 *** 0.02099609375 10009 *** 0.02099609375 10037 *** 0.02001953125 > 100003 *** 0.02490234375 100019 *** 0.02392578125 100043 *** 0.02392578125 > 1000003 *** 0.028076171875 1000033 *** 0.028076171875 1000037 *** 0.029052734375 > 10000019 *** 0.032958984375 10000079 *** 0.033203125 10000103 *** 0.032958984375 > 100000007 *** 0.0380859375 100000037 *** 0.0380859375 100000039 *** 0.0380859375 > 1000000007 *** 0.041015625 1000000009 *** 0.0419921875 1000000021 *** 0.0419921875
增长速度是O(log n),所以10^6附近应该是10^3附近所消耗时间的两倍,10^9是三倍:从上面的结果来看,10^6次方的数据比较接近(0.028/0.014),但10^9则要小了不少,只有大概2.67倍左右;10^8应该是10^4的两倍,这个数据也还比较接近(0.038/0.020)。
练习1.25
其实这个问题的答案在前面的脚注46中就说了:
这种技术非常有用,因为它意味着我们的计算中不需要去处理比m大很多的数(请与练习1.25比较)。
原来的 expmod 函数是利用了以下的等式:
(x * y) % m = [(x % m) * (y % m)] % m
这样,如果 x*y 的值很大的话,可以分解成两个小于m的数再取模,这样计算起来就要容易很多。
而1.25中的 expmod 的定义也是没问题的:先算出乘方值,再取模。但是需要注意的是,这个乘方值可能很大,这样再求模,可能就会很慢,没有办法和原来版本的高效性相提并论。
练习1.26
这个题还比较好理解,在使用 square 的时候,只需要在 expmod 内部执行一次递归调用,但直接使用乘法的话,会执行两次递归调用,情况如下:
| 次数 | 递归情况(square) | 递归情况(*) |
|---|---|---|
| 1 | n | n |
| 2 | n/2 | n/2 * n/2 |
| 3 | n/4 | n/4 * n/4 * n/4 * n/4 |
| … |
注:上表没有考虑 n-1 的情况,因为 n-1 作为常数级的衰减(请原谅,我自己发明了“衰减”这个词),和指数级衰减比起来可以忽略。
可以看到,使用 square 的情况是指数级衰减,所以最终是Θ(log n);直接使用乘法虽然也是指数级衰减,但是衰减的同时,递归调用数却在指数级增加,刚好和衰减抵消,于是就是Θ(n)。
练习1.27
这个题目比较简单,定义的两个函数如下:
(define (carmichael-check n a)
(cond ((not (= (expmod a n n) a)) false)
((> a 1) (carmichael-check n (- a 1)))
(else true)))
(define (carmichael-test n)
(carmichael-check n (- n 1)))
需要测试Carmichael数的时候,执行 carmichael-test 即可。这个测试有一点缺陷就是,不能把真正的质数和Carmichael数分开,不过题目是要求验证Carmichael数,而并不是求Carmichael数,所以这点缺陷也不算是缺陷。
练习1.28
这个题目是费马测试的一个变形,因为费马测试会被Carmichael数骗,所以这个Miller-Rabin检查增强了限制,Carmichael数也通不过检查。增强的条件是:如果大于1小于n - 1的一个数的平方取模n等于1,则n不是素数。这样,需要我们将费马测试中的 expmod 函数加以改进,所有相关的过程如下:
(define (determine-result a n)
(cond ((and (not (= a 1))
(not (= a (- n 1)))
(= (remainder (square a) n) 1)) 0)
(else (remainder (square a) n))))
(define (expmod base exp m)
(cond ((= exp 0) 1)
((even? exp)
(determine-result (expmod base (/ exp 2) m) m))
(else (remainder (* base (expmod base (- exp 1) m)) m))))
(define (miller-rabin-test n)
(define (try-it a)
(= (expmod a (- n 1) n) 1))
(try-it (+ 1 (random (- n 1)))))
(define (miller-rabin-prime? n times)
(cond ((= times 0) true)
((miller-rabin-test n) (miller-rabin-prime? n (- times 1)))
(else false)))
再用 miller-rabin-prime? 检测素数的时候,就算连561,1105等Carmichael数也无处遁形了。
练习1.29
定义两个过程如下:
(define (sum-simpson-rule f k n a b)
(define (factor)
(cond ((or (= k 0)
(= k n)) 1)
((= (remainder k 2) 0) 2)
(else 4)))
(if (> k n)
0
(+ (* (factor) (f (+ a (* k (/ (- b a) n)))))
(sum-simpson-rule f (+ 1 k) n a b))))
(define (simpson-rule f n a b)
(* (/ (/ (- b a) n) 3) (sum-simpson-rule f 0 n a b)))
经过测试,这个辛普森规则准得过分,在测试 cube 函数在0到1之间的积分时,n都不用取到100或者1000,就算取成2,结果也是精确的1/4。。。
练习1.30
采用迭代进行计算的 sum 过程如下:
(define (sum term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (+ (term a) result))))
(iter a 0))
练习1.31
递归的 product 过程:
(define (product term a next b)
(if (> a b)
1
(* (term a)
(product term (next a) next b))))
迭代的 product 过程:
(define (product term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (* (term a) result))))
(iter a 1))
factorial 过程:
(define (factorial n) (product (lambda (a) a) 1 (lambda (a) (+ 1 a)) n))
求圆周率PI的过程:
(define (cal-pi n)
(* 2.0 ;; 使用2.0而不用2,是为了让结果展示为小数而不是分数
(if (even? n) n (+ 1 n)) ;; 这个不可缺少,下面有解释
(/
(product (lambda (a) (square a))
2
(lambda (a) (+ 2 a))
(if (even? n) n (+ 1 n)))
(product (lambda (a) (square a))
3
(lambda (a) (+ 2 a))
(if (even? n) (+ 1 n) (+ 2 n))))))
书中给出的求PI公式比较tricky,将等式两边乘以2,就会发现形式比书中原来的形式要完美很多,上面的过程的基础正是乘以2后的等式。分别计算分子和分母,相除后,再乘以2,但要注意的是,这时的结果还不是圆周率,还需要乘以最后一个参加计算的分子值,为什么呢?因为我们最初为图方便(为了使用平方计算),把等式两边都乘以2,这样就硬生生把分子部分的序列给向后移了一位,所以要将原来被挤掉的分子最后一个参加计算的数字给补上。
练习1.32
递归的 accumulate 过程:
(define (accumulate combiner null-value term a next b)
(if (> a b)
null-value
(combiner (term a)
(accumulate combiner null-value term (next a) next b))))
迭代的 accumulate 过程:
(define (accumulate combiner null-value term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (combiner (term a) result))))
(iter a null-value))
利用 accumulate 进行重定义的 sum 和 product 过程:
(define (sum term a next b) (accumulate + 0 term a next b)) (define (product term a next b) (accumulate * 1 term a next b))
练习1.33
filtered-accumulate 过程以及根据其定义的求素数和、求互素正整数积的过程:
(define (filtered-accumulate combiner null-value term a next b filter)
(if (or (> a b) (not (filter a b)))
null-value
(combiner (term a)
(filtered-accumulate combiner null-value term (next a) next b filter))))
(define (sum-prime a b)
(filtered-accumulate + 0 (lambda (a) a) a (lambda (a) (+ 1 a)) b prime?))
(define (product-gcd-prime n)
(filtered-accumulate * 1 (lambda (a) a) 1 (lambda (a) (+ 1 a)) n gcd-eq1?))
练习1.34
如果求值 (f f) ,展开的流程如下:
(f f) => (f 2) => (2 2)
因为2不是一个过程名,所以出错。
练习1.35
x |-> 1 + 1/x 的不动点即要求满足 x = 1 + 1/x ,两边乘以x得到 x^2 = x + 1 ,即黄金分割满足的方程。
通过 fixed-point 来计算黄金分割率:
(fixed-point (lambda (x) (+ 1 (/ 1 x))) 0.5)
练习1.36
修改后的 fixed-point 过程:
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) 0.0000001))
(define (try guess)
(let ((next (f guess)))
(display next)
(newline)
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
不使用平均阻尼:
(fixed-point (lambda (x) (/ (log 1000) (log x))) 2)
使用平均阻尼:
(fixed-point (lambda (x) (average x (/ (log 1000) (log x)))) 2)
允许误差为10e-7的情况下,不使用平均阻尼需要46步,使用平均阻尼只需要13步。可见使用平均阻尼能大大减少必要的计算步数。
练习1.37
递归的 cont-frac 过程:
(define (cont-frac n d k)
(define (frac i)
(if (> i k)
0
(/ (n i)
(+ (d i) (frac (+ 1 i))))))
(frac 1))
迭代的 cont-frac 过程:
(define (cont-frac n d k)
(define (iter i result)
(if (< i 1)
result
(iter (- i 1)
(/ (n i)
(+ (d i) result)))))
(iter k 0))
用下面的lambda过程来确定满足条件的k:
((lambda (k)
(< (abs (- (/ 1 (cont-frac (lambda (i) 1.0)
(lambda (i) 1.0)
k))
1.61803401))
0.0001))
11)
最后确定,k取11即可保证4位的十进制精度。
练习1.38
这个题目最关键的是确定 D(i) 函数的值,观察规律,可以知道,序列中的3n项和3n+1项都是1,而3n+2项的值是2n+2,这里n是非负整数。所以,=D(i)= 相应的过程定义如下:
(define (d i)
(cond ((or (= (remainder i 3) 0)
(= (remainder i 3) 1)) 1)
(else (/ (* 2 (+ 1 i)) 3))))
用来求e的程序:
(+ 2 (cont-frac (lambda (i) 1.0) d 100000))
练习1.39
tan-cf 过程如下:
(define (tan-cf x k)
(define (n i)
(if (= i 1) x (square x)))
(define (d i)
(- (* 2 i) 1))
(define (cf i)
(if (> i k)
0
(/ (n i)
(- (d i) (cf (+ 1 i))))))
(cf 1))
练习1.40
(define (cubic a b c)
(lambda (x)
(+ (cube x)
(* a (square x))
(* b x)
c)))
练习1.41
double 过程:
(define (double f) (lambda (x) (f (f x))))
表达式的值是21,因为两次 double 调用就得到4层 double 嵌套的过程,再对 inc 作用,就会得到2的4次方,即16次 inc 过程的调用,所以结果是5 + 16 = 21。
练习1.42
(define (compose f g) (lambda (x) (f (g x))))
练习1.43
(define (repeated f n)
(if (<= n 1)
(lambda (x) (f x))
;(repeated (compose f f) (- n 1))
(compose f (repeated f (- n 1)))))
需要注意 repeated 和 compose 的调用顺序,如果先调用 compose 再调用 repeated (如代码中注释所示),那过程 f 会被重复2的n-1次方(注意是次方关系);但是反之,则 f 就只会被重复n次,是加和关系。
练习1.44
平滑过程 smooth :
(define dx 0.0000000001) (define (smooth f) (lambda (x) (/ (+ (f x) (f (- x dx)) (f (+ x dx))) 3)))
n次平滑过程 smooth-n :
(define (smooth-n f n) ((repeated smooth n) f))
练习1.45
经过一系列实验,有如下结果(箭头前的数字代表是几次方根,箭头后的数字是表明要做几次平均阻尼):
2, 3 => 1 4, 5, 6, 7 => 2 8, 9, 10, 11, 12, 13, 14, 15 => 3 16 ... ...
可以看到,需要做的平均阻尼的次数是对数级增长的,从2^n次方根到2^(n+1) - 1次方根需要做n次平均阻尼才可以保证不动点收敛(遗憾的是,本人无法对这一结论进行证明)。
写出求n次方根的过程如下:
(define (nth-root x n)
(fixed-point
((repeated average-damp
(floor (/ (log n) (log 2))))
(lambda (y) (/ x (expt y (- n 1))))) 1.0))
可以用以下的调用验证:
(nth-root (expt 2 100) 100)
即先求2的100次方再求其100次方根,结果是2说明过程没有错误。
练习1.46
iterative-improve 过程:
(define (iterative-improve good-enough? improve-guess)
(lambda (guess)
(let ((next (improve-guess guess)))
(if (good-enough? next guess)
next
((iterative-improve good-enough? improve-guess)
(improve-guess guess))))))
改进后的 sqrt 和 fixed-point 过程:
(define (sqrt x)
((iterative-improve (lambda (v1 v2) (< (abs (- v1 v2)) 0.0001))
(lambda (y) (average y (/ x y))))
1.0))
(define (fixed-point f first-guess)
((iterative-improve (lambda (v1 v2) (< (abs (- v1 v2)) 0.0001))
(lambda (y) (f y)))
first-guess))
构造数据抽象
练习2.1
(define (make-rat n d)
(define (make-rat-inner n d)
(let ((g (gcd n d)))
(cons (/ n g) (/ d g))))
(if (< (/ n d) 0)
(make-rat-inner (- (abs n)) (abs d))
(make-rat-inner (abs n) (abs d))))
练习2.2
(define (make-segment point-x point-y)
(cons point-x point-y))
(define (start-segment segment)
(car segment))
(define (end-segment segment)
(cdr segment))
(define (make-point x y)
(cons x y))
(define (x-point point)
(car point))
(define (y-point point)
(cdr point))
(define (midpoint-segment segment)
(make-point (average (x-point (start-segment segment))
(x-point (end-segment segment)))
(average (y-point (start-segment segment))
(y-point (end-segment segment)))))
练习2.3
(define (make-rectangle p-lu p-rd)
(cons p-lu p-rd))
(define (rect-left-up-point rect)
(car rect))
(define (rect-right-down-point rect)
(cdr rect))
(define (perimeter rect)
(* 2 (+ (- (x-point (rect-right-down-point rect))
(x-point (rect-left-up-point rect)))
(- (y-point (rect-left-up-point rect))
(y-point (rect-right-down-point rect))))))
(define (area rect)
(* (- (x-point (rect-right-down-point rect))
(x-point (rect-left-up-point rect)))
(- (y-point (rect-left-up-point rect))
(y-point (rect-right-down-point rect)))))
练习2.4
(define (cdr z) (z (lambda (p q) q)))
这三个过程充分利用了第一章讲的构造过程抽象: cons 返回一个过程,这个过程将一个参数过程作用于两个元素x和y上;于是,在定义 car 和 cdr 的时候,需要构造一个过程,分别返回第一个元素和第二个元素,然后把这个过程作为参数传递给 cons 返回的过程。
练习2.5
几个过程的定义如下:
(define (cons a b)
(* (expt 2 a) (expt 3 b)))
(define (a x n)
(if (= (remainder x n) 0)
(a (/ x n) n)
x))
(define (car z)
(define (d x n)
(if (= (remainder x n) 0)
(a (/ x n) n)
x))
(/ (log (d z 3))
(log 2)))
(define (cdr z)
(define (d x n)
(if (= (remainder x n) 0)
(a (/ x n) n)
x))
(/ (log (d z 2))
(log 3)))
不过这几个过程还是有缺陷的,只能用于整数,例如 (car (cons 1.2 3)) 就会返回不正确的结果,不过这是必然的。
练习2.6
初看到这个题目的时候,我的第一反应是“我操”(原谅我的粗口,但这确实是我的下意识反应。。),已经定义好的 zero 是一个过程,它会返回一个过程,返回的过程里面又会返回一个过程。。
硬着头皮看了看,后面有提示说可以按 (add-1 zero) 来求 one ,于是把这个调用展开,可以得到以下关于 one 的定义:
(define one (lambda (f) (lambda (x) (f x))))
和 zero 作了一下比较,第一眼发现是返回的过程的过程里面多了一个 f 调用,再观察 add-1 的定义,有理由相信接下来 two 的定义肯定是再多一个 f 调用,再利用 (add-1 one) 来展开一下,果然, two 的定义如下:
(define two (lambda (f) (lambda (x) (f (f x)))))
至此,这一切已经明确了,数字增长1,对 f 的调用多加一层即可。而且,根据 add-1 的定义,可以写出相应的 + 过程:
(define (+ a b) (lambda (f) (lambda (x) ((b f) ((a f) x)))))
别看这个过程只有两行,可是花了我不少时间,最初的版本我写成了 b(f)(a(f))(x) ,但实际的形式应该是: b(f)(a(f)(x)) (有点绕,大致意思是,a对f作用后的返回值,作为函数对x进行作用,然后将其返回值作为参数,传递给b对f作用后的返回值)。
另外有一点,因为这些数字的表示都是过程,所以不太好验证,所以需要构造一个 f 过程,能让它根据调用次数得到不同的值,本打算采用乘方,但乘方增大的过程太快;也没办法用加法,因为加法过程已经被我们给重定义了。所以选用了普通乘法,几个验证例子如下(注意把参数x的初始值置为1,以免干扰运算的结果):
((one (lambda (x) (* 2 x))) 1) => 2^1 = 2 (((add-1 one) (lambda (x) (* 2 x))) 1) => 2^(1+1) = 4 (((add-1 two) (lambda (x) (* 2 x))) 1) => 2^(2+1) = 8 (((+ two two) (lambda (x) (* 2 x))) 1) => 2^(2+2) = 16 (((+ (+ two two) one) (lambda (x) (* 2 x))) 1) => 2^(2+2+1) = 32
以我个人的意见,这个题目算是把第一章“构造过程抽象”的思想用到极致了的,第一章后面的习题跟这个相比,简直是小巫见大巫。而且,这个题目也很有意思,数字的表示不再是传统的计数方式,而是用过程调用次数来表示。
练习2.7
(define (upper-bound z) (cdr z)) (define (lower-bound z) (car z))
练习2.8
根据之前的 add-interval 和 mul-interval 来看,对两个区间操作的结果,是这样一个区间:其下界是两个区间分别取一个点执行相应操作的可能取的最小值,而上界则是相应的可能的最大值。
所以,对于减操作一样,需要确定两个区间中点相减的可能最小值与最大值,这就是新区间的界。假设两个区间分别为[a1, b1]和[a2, b2],那么,有以下结论:
a1 - a2 > a1 - b2 b1 - a2 > b1 - b2 b1 - a2 > a1 - a2 b1 - b2 > a1 - b2
所以,很容易就可以看出,新区间的下界是 a1 - b2 ,上界是 b1 - a2 ,于是,有以下定义:
(define (sub-interval x y)
(make-interval (- (lower-bound x) (upper-bound y))
(- (upper-bound x) (lower-bound y))))
练习2.9
对于加法和减法的证明,实在是不能再简单了,所以这里也就不写了,最后结果是,和和差的宽度都是两个操作数的宽度的算术平均值。至于乘和除,从定义上就可以看出来,其上界和下界的确定有一定的随机性(不像加和减,能完完全全推导出其上界和下界),所以,其宽度自然也不会是关于两个操作数的宽度的函数。
练习2.10
(define (div-interval x y)
(if (and (<= (lower-bound y) 0)
(>= (upper-bound y) 0))
(error "cannot divide an interval contains zero.")
(mul-interval
x
(make-interval (/ 1.0 (upper-bound y))
(/ 1.0 (lower-bound y))))))
练习2.11
说实话,我个人觉得这个题目挺没意思的,原来的 mul-interval 的实现就是为了避免出现要区分区间边界正负的情况,而这个题目则要求把这些情况一一列出来。。
如此实现的唯一理由就是减少乘法的执行次数来提高效率,但个人认为这点效率的提升和代码的可读性及简洁程度相比根本不算什么,而且,其实也提升不了多少性能,改写之后至少也需要两次乘法,而原来的实现也只有四次乘法而已。。
所以,我就不实现了,只列出所有的可能(以a/b分别代表两个区间,L/M/R分别代表区间全在负半轴、区间跨零点,区间全在正半轴的情况):
aL, bL aL, bM aL, bR aM, bL aM, bM aM, bR aR, bL aR, bM aR, bR
其实就是简单的排列组合而已。这里并没有单独考虑区间边界正好是零点的情况,因为这种情况并没有特殊性,若左边界为零点,可将其归到R,同理,若右边界为零点,可将其归到L。
练习2.12
(define (make-center-percent c p) (make-interval (- c (* c p)) (+ c (* c p)))) (define (percent i) (/ (width i) (center i)))
练习2.13
这个证明还比较简单,假设两个区间的中点和误差百分比分别为c1, p1和c2, p2,所以,两个区间可以表示为:
i1 = [c1 - c1 * p1, c1 + c1 * p1] i2 = [c2 - c2 * p2, c2 + c2 * p2]
而题目假设所有的数为正,所以,区间相乘的下界即为原来的区间的下界相乘,上界即为原来的上界相乘,新区间如下:
i = i1 * i2 = [(c1 - c1 * p1)(c2 - c2 * p2), (c1 + c1 * p1)(c2 + c2 * p2)] = [c1c2 - c1c2p1 - c1c2p2 + c1c2p1p2, c1c2 + c1c2p1 + c1c2p2 + c1c2p1p2]
所以,按照定义,新生成的区间的百分比误差为:
p = width / center = (ub - lb) / (ub + lb) = ... = (p1 + p2) / (1 + p1 * p2)
上面的计算公式中, width 和 center 分别代表新生成区间宽度和中点, ub 和 lb 分别代表新生成区间的上界和下界。中间的具体计算步骤比较难用纯文字表达,所以略去,其实也不难,将相应的值代入计算即可。
可以看到,最后的误差百分比跟原来的中点c1和c2是没有关系的,命题即得证。
练习2.14
根据给出的 par1 和 par2 过程的定义,作如下验证:
(par1 (make-center-percent 1 0.05)
(make-center-percent 2 0.02))
(par2 (make-center-percent 1 0.05)
(make-center-percent 2 0.02))
结果如下:
> '(0.6025889967637541 . 0.7360824742268043) > '(0.6398625429553264 . 0.6932038834951456)
可以看到,两次的结果确实不同。
练习2.15
个人感觉,这个说法是站不住脚的。因为,根据当前的区间四则运算定义,数据精度的损失是跟计算次数有关的,而不是跟什么非准确性变量的出现次数有关。
根据
par1 和 par2 的定义可以看出,前者使用了三次区间运算,而后者使用了四次运算,所以后者的精度要比前者差。
感觉上面的想法不靠谱,于是去google了一下这个题目,才发现“真理”跟我的想法完全不同:我以为所谓的精度损失是跟计算机无法完全表示浮点数有关,在计算的过程中逐渐损失了精度,但事实上,根本就没有所谓的精度,也跟计算机的浮点计算精度没有任何关系!!
根本原因是因为,我们的计算对象本来就是一个不确定具体值的区间,所以,在将两个区间进行相加和相乘操作的时候,无形中扩大了区间的宽度,也改变了误差百分比!!但是有一点需要注意的是,并不是所有的区间计算都会改变宽度,“元区间”(我自己起的名字) [1, 1] 就不会增加宽度,其它的“非准确性变量”都会改变区间宽度。所以,题目中的Eva Lu Ator的说法是对的,非准确性变量出现得越少,最后生成的区间就越紧凑。根据这个观点, par2 总共有四次计算,其中三次都有元区间参与而只有一次是两个非准确性变量参与;而 par1 的三次计算全部都是非准确性变量参与的,所以确实 par2 是比 par1 更好的程序。
练习2.16
这个题目就更进一步,让我们自行设计一套针对区间的计算法则,让在数学上等价的计算公式通过我们的计算法则能算出相同的结果。
受练习2.13的启发,我想能否设计出针对一个区间的中点c和误差百分比p分别进行计算的四则运算法则,在分别运算完成之后,再将计算所得结果的中点C和误差百分比P组合起来得到结果区间。但后来再想了想,发现不太可行,就拿2.13的结论来说,两个区间相乘,结果的误差百分比 p = (p1 + p2) / (1 + p1 * p2) ,如果p1和p2足够小,上面的等式就近似等于 p = p1 + p2 ,这就意味着,结果区间的误差百分比是两个因子区间误差百分比的和,从而必然导致区间的扩大。自然而然,通过数学上等价的公式计算的结果也不会相同。
后来再深入地想了想,这种问题的出现,是因为区间运算的约束条件所造成的,以乘法为例,要确保约束条件满足(即结果区间必须要包含因子区间所有可能取值的乘积),就必然会导致区间的扩大。所以,只要设计出来的计算法则满足区间计算的约束条件,那么无论怎么精心设计,都会碰上这一不可避免的问题。
PS:这个题目的后面有一个警告,说是这个问题非常难,所以,我就不再去深究了,以我目前的数学水平,还达不到深入研究这一问题的层次。。
练习2.17
(define (last-pair items)
(if (or (null? items) (null? (cdr items)))
items
(last-pair (cdr items))))
练习2.18
(define (reverse items)
(if (null? items)
items
(append (reverse (cdr items)) (list (car items)))))
练习2.19
(define (first-denomination coin-values) (car coin-values)) (define (except-first-denomination coin-values) (cdr coin-values)) (define (no-more? coin-values) (null? coin-values))
算法中根本就没有涉及到有关硬币顺序的内容,所以表 coin-values 的顺序显然不会影响最后的结果。
练习2.20
这个题目还很花了我一点时间。。主要是这货不是普通的 if...else... 型的简单的递归调用,而是有三个分支,而且递归终止条件也不太好控制。。
(define (same-parity . items)
(define (sp? a b)
(cond ((and (odd? a) (odd? b)) true)
((and (even? a) (even? b)) true)
(else false)))
(define (sp a others)
(cond ((null? others) (list a))
((sp? a (car others)) (append (list a)
(sp (car others) (cdr others))))
(else (sp a (cdr others)))))
(if (null? items)
items
(sp (car items) (cdr items))))
练习2.21
(define (square-list items)
(if (null? items)
'()
(cons (expt (car items) 2) (square-list (cdr items)))))
(define (square-list items)
(map (lambda (x) (expt x 2))
items))
练习2.22
两种实现都是有问题的,例如对于如下调用:
(square-list '(1 2 3))
两种实现的展开过程分别如下:
;; implementation 1 => (iter '(1 2 3) nil) => (iter '(2 3) '(1)) => (iter '(3) '(4 1)) => (iter '() '(9 4 1)) => '(9 4 1)
;; implementation 2 => (iter '(1 2 3) nil) => (iter '(2 3) '(nil . 1)) => (iter '(3) '((nil . 1) . 4)) => (iter '() '(((nil . 1) . 4) . 9)) => '(((nil . 1) . 4) . 9)
练习2.23
(define (for-each proc items)
(if (null? items)
'()
(begin (proc (car items))
(for-each proc (cdr items)))))
练习2.24
这个题目的结果是 (1 (2 (3 4))) ,和图2-5刚好相反,图2-5是 car 复杂, cdr 简单,这个题目是 cdr 复杂, =car=简单。
这个结构图和树状图就不画了,只用纯文本画不出来,我画书上了。。
练习2.25
(car (cdr (car (cdr (cdr '(1 3 (5 7) 9)))))) (car (car '((7)))) (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr '(1 (2 (3 (4 (5 (6 7))))))))))))))))))
练习2.26
(append x y) = (1 2 3 4 5 6) (cons x y) = ((1 2 3) 4 5 6) (list x y) = ((1 2 3) (4 5 6))
练习2.27
被这个题坑了好久才做出来。。这个题需要注意的是,假设x是 ((1 2) (3 4)) 的话,那么 (car x) 返回 (1 2) ,而 (cdr x) 返回 ((3 4)) !!千万不要以为 car 和 cdr 是对等的!!前者是取元素,而后者是取剩下的表!!我就是坑在这一点上,在线性表的时候,这个坑还算比较小,如果是一棵树的话,这个坑就大了。。
(define (deep-reverse items)
(cond ((not (pair? items)) items)
((null? (cdr items)) (list (deep-reverse (car items))))
(else (append (deep-reverse (cdr items)) (list (deep-reverse (car items)))))))
在上述代码中,有两个地方都对 car 进行了 list 包装处理,这是因为,按前面例子中所说的, car 只取出一个元素,所以,在结果中需要重新将其包装成一个表,而 cdr 取出的本身就是一个表,所以不需要包装。
练习2.28
这个题又是一个坑,不过有了上题的经验,这一题就好控制多了,与上一题不同的是,这一题用迭代来完成,因为要将树形的结构给转换成线性表,所以需要一个“全局”变量来存储中间转换结果,迭代是最适合的,用递归的话,可能需要 let 声明,而我是比较讨厌 let 的,能尽量不用就尽量不用。。
(define (fringe items)
(define (iter items result)
(cond ((null? items) result)
((not (pair? items)) (append result (list items)))
(else (iter (cdr items) (iter (car items) result)))))
(iter items '()))
练习2.29
a) 这几个过程还是相对比较简单的,取对应元素即可,需要注意的是,在取活动体右边的部分时,要用 cadr 而不是 cdr 。
(define (left-branch mobile) (car mobile)) (define (right-branch mobile) (cadr mobile)) (define (branch-length branch) (car branch)) (define (branch-structure branch) (cadr branch))
b) total-weight 过程如下:
(define (total-weight mobile)
(cond ((null? mobile) 0)
((not (pair? mobile)) mobile)
(else (+ (total-weight (branch-structure (left-branch mobile)))
(total-weight (branch-structure (right-branch mobile)))))))
c) 用于检查平衡的 check-balance 过程如下:
(define (check-balance mobile)
(cond ((null? mobile) #f)
((not (pair? mobile)) #t)
((not (= (* (branch-length (left-branch mobile))
(total-weight (branch-structure (left-branch mobile))))
(* (branch-length (right-branch mobile))
(total-weight (branch-structure (right-branch mobile))))))
#f)
(else (and (check-balance (branch-structure (left-branch mobile)))
(check-balance (branch-structure (right-branch mobile)))))))
d) 起初我以为要大修改才能达到要求,但仔细看了看,跟底层具体数据结构相关的只有在a)中定义的那几个选择过程,而b)和c)中的过程都是构建在a)中的选择过程之上,所以并不会受到影响,因此只需要简单改a)中的四个选择过程即可。
练习2.30
(define (square-tree tree)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(square-tree sub-tree)
(expt sub-tree 2)))
tree))
(define (square-tree tree)
(cond ((null? tree) #nil)
((not (pair? tree)) (expt tree 2))
(else (cons (square-tree (car tree))
(square-tree (cdr tree))))))
练习2.31
(define (tree-map proc tree)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(tree-map proc sub-tree)
(proc sub-tree)))
tree))
练习2.32
这个解法,就是典型的分治算法,跟第一章那个硬币换零钱有点像,把看似无处下手的大问题硬生生化成多个小问题,再逐个解决。
思路:除空集外,一个集合的子集,必然由以下两部分组成:
- 除第一个元素外,其它元素形成的集合的所有子集
- 上一条中,所有子集再加入第一个元素所形成的所有集合
有人问,那由第一个元素单独形成的集合怎么办,其实包含在第二条中了,因为第一条中的子集有空集,所以再利用第二条的规则,就可以得到只包含第一个元素的集合。
下面的解法正是由此而来:
(define (subsets s)
(if (null? s)
(list #nil)
(let ((rest (subsets (cdr s))))
(append rest
(map (lambda (set)
(append set (list (car s))))
rest)))))
练习2.33
(define (map p sequence) (accumulate (lambda (x y) (cons (p x) y)) #nil sequence)) (define (append seq1 seq2) (accumulate cons seq2 seq1)) (define (length sequence) (accumulate (lambda (x y) (+ y 1)) 0 sequence))
练习2.34
(define (hornor-eval x coefficient-sequence)
(accumulate (lambda (this-coeff higher-terms)
(+ this-coeff (* x higher-terms)))
0
coefficient-sequence))
练习2.35
(define (count-leaves tree)
(accumulate (lambda (x y) (+ x y))
0
(map (lambda (x) (length (enumerate-tree x)))
tree)))
练习2.36
(define (accumulate-n op init seqs)
(if (null? (car seqs))
#nil
(cons (accumulate op init (map car seqs))
(accumulate-n op init (map cdr seqs)))))
练习2.37
关于矩阵运算基本都忘光了,这个题目中的定义又不太清楚,摸索了老半天才战战兢兢地写出答案(其实矩阵和行向量不太能相乘的,因为矩阵乘法规定第一个矩阵的列数和第二个矩阵的行数必须相等,如果矩阵乘以行向量,那这个矩阵必须是列向量才行):
(define (dot-product v w)
(accumulate + 0 (map * v w)))
(define (matrix-*-vector m v)
(map (lambda (row)
(dot-product v row)) m))
(define (transpose mat)
(accumulate-n cons #nil mat))
(define (matrix-*-matrix m n)
(let ((cols (transpose n)))
(map (lambda (row)
(matrix-*-vector n row)) m)))
练习2.38
fold-left 和 fold-right 不相同的不仅仅是累计作用的顺序,还有两个操作数的顺序也相反:
(fold-left list #nil '(1 2 3)) ;; -> (((#nil 1) 2) 3) (fold-right list #nil '(1 2 3)) ;; -> (1 (2 (3 #nil)))
前者产生的第一个序列是 (#nil 1) ,而后者产生的第一个序列是 (3 #nil) ,由此可以看出,操作数的顺序也是相反的。
所以,要想 fold-left 和 fold-right 产生相同的结果,那么 op 操作只要满足交换律即可,比如 + 或者 * 。
练习2.39
(define (reverse1 sequence) (fold-right (lambda (x y) (append y (list x))) #nil sequence)) (define (reverse2 sequence) (fold-left (lambda (x y) (cons y x)) #nil sequence))
练习2.40
(define (unique-pairs n)
(flatmap (lambda (i)
(map (lambda (j) (list i j))
(enumerate-interval 1 (- i 1))))
(enumerate-interval 1 n)))
练习2.41
在定义 unique=triples 的时候借用了前面的 flatmap ,但由于 flatmap 只能除去多余的一层括号,而我们的三元组有三层嵌套映射,比二元组多了一层,所以需要在外面再加上一层 accumulate 来去除多出来的一层括号。
(define (unique-triples n)
(accumulate append
#nil
(flatmap (lambda (i)
(map (lambda (j)
(map (lambda (k) (list i j k))
(enumerate-interval 1 (- j 1))))
(enumerate-interval 1 (- i 1))))
(enumerate-interval 1 n))))
(define (const-sum-triples n s)
(filter (lambda (item)
(= s (+ (car item) (cadr item) (caddr item))))
(unique-triples n)))
练习2.42
这个是经典的八皇后问题,题目把框架给写好了,我们只需要填好 empty-board 变量、 adjoin-position 过程以及 safe? 过程即可。不过这个框架抽象程度比较高,要看懂还不太容易。。
废话少说,其实这个框架设计得是很巧妙的:它已经把数据层给我们剥离开来了,也就是说,跟数据结构相关的过程都要我们自己实现,这样,就算采用不同的数据结构来表示棋盘构造和皇后位置,只要上面的两个过程和一个变量逻辑正确,这个框架也是可以正常工作的,这就是数据抽象的威力!!
我的数据结构:本来是打算构建一个向量,第k个元素代表第k列的皇后的行数,但是这个向量在 safe? 过程中操作有点麻烦,于是把这个向量给颠倒了过来,第k个元素代表第n-k+1列皇后的行数,这样在 safe? 过程中就好操作多了。按道理,在最后的结果中,还是要把这个向量给再颠倒过来的,但是由于对称的关系,如果存在一个解 (5 2 4 7 3 8 6 1) 的话,那么必然存在解 (1 6 8 3 7 4 2 5) ,所以没必要再给颠倒回来。
相关的代码如下:
(define empty-board #nil)
(define (adjoin-position new-row k rest-of-queens)
(append (list new-row) rest-of-queens))
(define (safe? k positions)
(define (iter k row c pos)
(cond ((null? pos) #t)
((or (= row (car pos))
(= (abs (- row (car pos)))
(abs (- k c)))) #f)
(else (iter k row (- c 1) (cdr pos)))))
(iter k (car positions) (- k 1) (cdr positions)))
练习2.43
这个题目,开始看了半天没看出来为什么:假设 (queen-cols k) 的解有 f(k) 个,那么一个是内层循环n次,外层循环f(k-1)次;另一个是内层循环f(k-1)次,外层循环n次,看起来好像没有区别。。于是把这两层循环换了一下,果然慢。。
又看了半天,终于看出点眉目了:正常的解的内层循环代价很小,但是Louis的解的内层是递归调用,所以代价很大! (queen-cols k) 需要调用n次 (queen-cols (- k 1)) ,而 (queen-cols (- k 1)) 又需要调用n次 (queen-cols (- k 2)) ,如此递归下去,可以推出: (queen-cols k) 最终调用了n的n次方次 (queen-cols 0) (因为到这一级才是常数级调用,所以要一直展开到这一级)!!
所以,如果正常解的时间为T的话,那么Louis的解针对8x8的棋盘就是 8^8 * T 。。
练习2.44
(define (up-split painter n)
(if (= n 0)
painter
(let ((smaller (up-split painter (- n 1))))
(below painter (beside smaller smaller)))))
练习2.45
(define (split proc1 proc2)
(lambda (painter n)
(if (= n 0)
painter
(let ((smaller ((split proc1 proc2) painter (- n 1))))
(proc1 painter (proc2 smaller smaller))))))
练习2.46
(define (make-vect x y)
(cons x y))
(define (xcor-vect vect)
(car vect))
(define (ycor-vect vect)
(cdr vect))
(define (add-vect vect1 vect2)
(make-vect (+ (xcor-vect vect1)
(xcor-vect vect2))
(+ (ycor-vect vect1)
(ycor-vect vect2))))
(define (sub-vect vect1 vect2)
(make-vect (- (xcor-vect vect1)
(xcor-vect vect2))
(- (ycor-vect vect1)
(ycor-vect vect2))))
(define (scale-vect s vect)
(make-vect (* s (xcor-vect vect))
(* s (ycor-vect vect))))
练习2.47
方案1:
(define (origin-frame frame) (car frame)) (define (edge1-frame frame) (cadr frame)) (define (edge2-frame frame) (caddr frame))
方案2(和方案1仅仅只有 edge2-frame 的定义不同):
(define (origin-frame frame) (car frame)) (define (edge1-frame frame) (cadr frame)) (define (edge2-frame frame) (cddr frame))
练习2.48
(define (make-segment start-vect end-vect) (cons start-vect end-vect)) (define (start-segment segment) (car segment)) (define (end-segment segment) (cdr segment))
练习2.49
这个题目,只需要学好高中数学的向量部分就可以做了。
对于a)、b)、c)三个小题,基本是一样的,都需要先确定四个基本点,然后根据这四个基本点调用 make-segment 产生线段再交给 segments->painter 即可。其中a)和b)需要确定的是框架的四个顶点;c)需要确定的是框架四条边的中点。
确定四个顶点和四个中点都是很容易的,假设三个基本向量分别为 origin 、 edge1 、 edge2 ,那么四个顶点和四个中点分别可以表示为:
origin origin + edge1 origin + edge2 origin + edge1 + edge2
origin + 0.5 * edge1 origin + 0.5 * edge2 origin + edge2 + 0.5 * edge1 origin + edeg1 + 0.5 * edge2
所以,很容易写出前三个小题的解答:
(define (border-painter frame)
(let ((point1 (origin-frame frame))
(point2 (add-vect (origin-frame frame)
(edge1-frame frame)))
(point3 (add-vect (origin-frame frame)
(edge2-frame frame)))
(point4 (add-vect (origin-frame frame)
(edge1-frame frame)
(edge2-frame frame))))
((segments->painter (list (make-segment point1 point2)
(make-segment point1 point3)
(make-segment point2 point4)
(make-segment point3 point4)))
frame)))
(define (cross-painter frame)
(let ((point1 (origin-frame frame))
(point2 (add-vect (origin-frame frame)
(edge1-frame frame)))
(point3 (add-vect (origin-frame frame)
(edge2-frame frame)))
(point4 (add-vect (origin-frame frame)
(edge1-frame frame)
(edge2-frame frame))))
((segments->painter (list (make-segment point1 point4)
(make-segment point2 point3)))
frame)))
(define (middle-point-painter frame)
(let ((middle-point1 (add-vect (origin-frame frame)
(scale-vect 0.5 (edge1-frame frame))))
(middle-point2 (add-vect (origin-frame frame)
(scale-vect 0.5 (edge2-frame frame))))
(middle-point3 (add-vect (origin-frame frame)
(edge2-frame frame)
(scale-vect 0.5 (edge1-frame frame))))
(middle-point4 (add-vect (origin-frame frame)
(edge1-frame frame)
(scale-vect 0.5 (edge2-frame frame)))))
((segments->painter (list (make-segment middle-point1 middle-point2)
(make-segment middle-point2 middle-point3)
(make-segment middle-point3 middle-point4)
(make-segment middle-point4 middle-point1)))
frame)))
对于小题d),我就不想再说什么了。。我数了一下,总共有17条线段。。而且,每条线段顶点的位置(注意是每条)都不是一眼能看出来的。。所以。。我们得首先拿直尺量出34个点的准确位置。。而我没有直尺。。所以。。我就不做了。。哪位有直尺、有兴趣、有闲情逸致的,可以慢慢去量。。
练习2.50
这个题目训练的就是空间想象能力(其实还不是空间,只是二维的),而这刚好是我的强项。。
从 flip-vert 的定义可以看到,它是将 origin 变换为 origin + edge2 ,然后 edge1 保持不变(看起来好像是变化了,但是因为要减去new origin,所以新的edge1和原来的edge1其实是同一个向量),再将 edge2 反向。所以,我们的 flip-horiz 要做的,就是将 origin 变换为 origin + edge1 ,然后 edge2 保持不变,将 edge1 反向:
(define (flip-horiz painter)
(transform-painter painter
(make-vect 1.0 0.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0)))
对于旋转变换,需要先说一点的是,书中的
rotate90 定义其实是顺时针旋转90度,并不是逆时针,因为它的变换为:将 origin 变换为 origin + edge1 ,将 edge1 变换为 edge2 ,将 edge2 变换为 edge1 反向,从直观来看,这就是顺时针旋转90度才有的结果。
后来仔细看了看,发现,我自己想象中的 edge1 和 edge2 跟书中画的那个frame的 edge1 和 edge2 位置相好相反,正因为如此,所以,才会觉得 rotate90 是顺时针旋转90度。。各位不妨把 edge1 和 edge2 交换个位置再试试,怎么样,是不是现在 rotate90 变成顺时针90度旋转了。。
既然如此,我们就照葫芦画瓢好了,对于逆时针180度的旋转,变换如下:将 origin 变换为 origin + edge1 + edge2 ,将 edge1 和 edge2 都反向,代码如下:
(define (rotate180 painter)
(transform-painter painter
(make-vect 1.0 1.0)
(make-vect 0.0 1.0)
(make-vect 1.0 0.0)))
对于逆时针270度旋转,其实等价于顺时针90度旋转,变换如下:将 origin 变换为 origin + edge2 ,将 edge1 变换为 edge2 反向,将 edge2 变换为 edge1 ,代码如下:
(define (rotate270 painter)
(transform-painter painter
(make-vect 0.0 1.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0)))
练习2.51
模仿 beside 的定义,可以得到下面的 below 定义:
(define (below painter1 painter2)
(let ((paint-bottom
(transform-painter painter1
(make-vect 0.0 0.0)
(make-vect 1.0 0.0)
(make-vect 0.0 0.5)))
(paint-top
(transform-painter painter2
(make-vect 0.0 0.5)
(make-vect 1.0 0.5)
(make-vect 0.0 1.0))))
(lambda (frame)
(paint-top frame)
(paint-bottom frame))))
对于利用利用 beside 和 rotate* 函数来定义 below 函数,需要注意要先将两个painter顺时针旋转90度,再整体逆时针旋转90度,如下:
(define (below painter1 painter2) (rotate90 (beside (rotate270 painter1) (rotate270 painter2))))
练习2.52
a) 在练习2.49中我们就没有做,因此,这里也略过。。
b) 其实这个题目我不大会,实在想不出如何只用 up-split 的一个副本,通过Google搜索得到了一个答案,但是感觉会和原来的图不太一样,如下:
(define (corner-split painter n)
(if (= n 0)
painter
(let ((up (up-split painter (- n 1)))
(right (right-split painter (- n 1)))
(corner (corner-split painter (- n 1))))
(beside (below painter up)
(below right corner)))))
c) 这个就不多说了,代码如下:
(define (square-limit painter n)
(let ((combine4 (square-of-four identity flip-horiz
flip-vert rotate180)))
(combine4 (corner-split painter n))))
练习2.53
(a b c) ((george)) ((y1 y2)) (y1 y2) #f #f (red shoes blue socks)
练习2.54
(define (equal? seq1 seq2)
(if (and (pair? seq1)
(pair? seq2))
(and (equal? (car seq1) (car seq2))
(equal? (cdr seq1) (cdr seq2)))
(eq? seq1 seq2)))
练习2.55
(car ''abracadabra) 等价于 (car (quote (quote abracadabra))) ,这个表达式第二个元素求值的结果就是列表 (quote abracadabra) ,所以再通过 car 来取首元素的话,结果自然会是 quote 。
练习2.56
对于指数求导,将其符号表示定义为 (** base exp) ,剩下的基本也就是照葫芦画瓢,定义好相应的几个过程,在 deriv 过程里面再加一个分支来表示指数求导就可以了:
(define (exponentiation? x)
(and (pair? x) (eq? (car x) '**)))
(define (base e) (cadr e))
(define (exponent e) (caddr e))
(define (make-exponentiation b e)
(cond ((=number? e 0) 1)
((=number? e 1) b)
(else (list '** b e))))
修改后的 deriv 过程:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
((exponentiation? exp)
(make-product (make-product (exponent exp)
(make-exponentiation (base exp)
(- (exponent exp) 1)))
(deriv (base exp) var)))
(else
(error "unknown expression type -- DERIV" exp))))
练习2.57
开始我把这题想复杂了,将和与积相关的好多过程都重定义了一遍,结果证明这是没有必要的,例如对于表达式 (+ x y z) ,它会被分开成 x 和 (+ y z) 分别进行求导,再将结果利用 make-sum 给加起来。对于 (+ y z) 的求导结果来讲,它是独立的,所以 make-sum 过程不需要作任何修改,只需要修改 augend 过程,让其能产生正确的 (+ y z) 即可。同理, multiplicand 也需要作相应修改:
(define (augend s)
(let ((a (cdr (cdr s))))
(cond ((< (length a) 2) (car a))
(else (cons '+ a)))))
(define (multiplicand p)
(let ((m (cdr (cdr p))))
(cond ((< (length m) 2) (car m))
(else (cons '* m)))))
上面代码中引入 cond 进行条件判断的原因是,对于 (+ x y z) ,需要被拆成 x 和 (+ y z) ,但对于 (+ y z) ,就只需要被拆成 y 和 z ,而不是 y 和 (+ z) ,所以需要引入参数个数的条件判断。
练习2.58
a) 这个小题比较简单,之前所使用的是前缀表达式,现在要换成中缀表达式,所以,需要修改几个构造和访问表达式的过程,如下:
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2) (+ a1 a2)))
(else (list a1 '+ a2))))
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list m1 '* m2))))
(define (sum? x)
(and (pair? x) (eq? (cadr x) '+)))
(define (addend s) (car s))
(define (product? x)
(and (pair? x) (eq? (cadr x) '*)))
(define (multiplier p) (car p))
b) 这个小题如题目中所说,确实比较难,相当于我们要实现一个小型的数学语法解析器,我写了三次,终于能正常工作了,以 (x + x * y + x) 为例,我第一次的实现,在遇到 x * y + x 的时候,没能正常处理运算符优先级,直接按从左到右的顺序解析,所以实际上解析成了 x * (y + x) ;第二次的实现,考虑了运算优先级,但是实际解析成了 x * y ,把后面的那个x漏掉了,因为虽然局部的优先级考虑了,整体的优先级还是错误的,直接导致后面的x被忽略了。经过两次坑,总结了一下,终于找到以下规则:
- 在有加法运算符存在的时候,整个表达式必须视为加法运算,否则就会出现上面的漏掉部分表达式的问题
- 乘法和加法混合的优先级不用考虑,因为在需要求乘数和被乘数的时候,整个表达式里面已经没有加法运算符了
除了上面两点之外,还有一些小坑,不过都是比较常规的序列的组织问题,不一一细述。另外,我还写了两个辅助过程 prefix-sub-exp 和 suffix-sub-exp ,用来求以某个符号分隔的一个序列的前缀和后缀。前者是给我第二次的错误尝试用的,用以从类似 (x * y + x) 的表达式中解析出 (x * y) ,在正确解中实际上它并没有被用到。
所有需要修改或者重新定义的过程如下(需要特别指出的是, deriv 过程本身并不需要任何修改,我想,大概这就是数据抽象的威力吧):
(define (prefix-sub-exp exp sep)
(define (iter exp sub)
(cond ((or (null? exp)
(eq? (car exp) sep))
sub)
(else (iter (cdr exp) (append sub (list (car exp)))))))
(iter exp '()))
(define (suffix-sub-exp exp sep)
(cond ((null? exp) '())
((eq? (car exp) sep) (cdr exp))
(else (suffix-sub-exp (cdr exp) sep))))
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2) (+ a1 a2)))
(else (let ((s1 (if (or (variable? a1)
(number? a1))
(list a1 '+)
(append a1 '(+))))
(s2 (if (or (variable? a2)
(number? a2))
(list a2)
a2)))
(append s1 s2)))))
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list m1 '* m2))))
(define (sum? x)
(and (pair? x)
(not (null? (filter (lambda (e) (eq? e '+)) x)))))
(define (addend s)
(let ((r (prefix-sub-exp s '+)))
(if (< (length r) 2) (car r) r)))
(define (augend s)
(let ((r (suffix-sub-exp s '+)))
(if (< (length r) 2) (car r) r)))
(define (product? x)
(and (pair? x) (eq? (cadr x) '*)))
(define (multiplier p) (car p))
(define (multiplicand p)
(let ((r (cdr (cdr p))))
(cond ((< (length r) 2) (car r))
(else r))))
实际上,我又对这个小程序作了第四次修改,改动源于我在测试以下调用的时候:
(deriv '(x + (x + x) * 1 * y) 'x)
发现结果是:
(1 + 2 * (1 * y))
这样的结果中还有多余的括号,还没有达到题目中的要求,所以需要像 make-sum 那样,对 make-product 过程再进行加工,修改后的代码如下(加入了是否需要去除多余括号的判断):
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (let ((p1 (cond ((or (variable? m1) (number? m1))
(list m1 '*))
((sum? m1) (list m1 '*))
(else (append m1 '(*)))))
(p2 (cond ((or (variable? m2) (number? m2))
(list m2))
((sum? m2) (list m2))
(else m2))))
(append p1 p2)))))
练习2.59
(define (union-set set1 set2)
(cond ((null? set1) set2)
((null? set2) set1)
((not (element-of-set? (car set1) set2))
(cons (car set1)
(union-set (cdr set1) set2)))
(else (union-set (cdr set1) set2))))
练习2.60
对于这种类型的集合,只需要重新定义 adjoin-set 和 union-set 两个过程即可:
(define (adjoin-set x set) (cons x set)) (define (union-set set1 set2) (append set1 set2))
因为简化的是插入和求并集操作,所以在这两个操作比较多的时候,使用有重复元素的集合会比较好。
练习2.61
(define (adjoin-set x set)
(define (insert x head tail)
(cond ((null? tail) (append head (list x)))
((< x (car tail)) (append head (list x) tail))
(else (insert x (append head (list (car tail))) (cdr tail)))))
(if (element-of-set? x set)
set
(cond ((null? set) (list x))
((< x (car set)) (cons x set))
(else (insert x (list (car set)) (cdr set))))))
练习2.62
(define (union-set set1 set2)
(cond ((null? set1) set2)
((null? set2) set1)
(else
(let ((x1 (car set1))
(x2 (car set2)))
(cond ((= x1 x2) (cons x1
(union-set (cdr set1)
(cdr set2))))
((< x1 x2) (cons x1
(union-set (cdr set1)
set2)))
((> x1 x2) (cons x2
(union-set set1
(cdr set2)))))))))
由于 union-set 是 intersection-set 的反操作,所以模仿 interseciont-set 即可构造出 union-set 过程。
练习2.63
a) 本来以为这两个过程会产生不同的结果的,但试了一下,结果是一样的。。第一个过程好理解,先遍历左子树,然后访问根,再遍历右子树;第二个过程采用了两次迭代,看起来要麻烦一点,但是从整体看,还是比较好理解的:先把右子树放到 result-list 里面,再把根加进去放到第一个,再把左子树加进去,至于左子树加的位置,因为 copy-to-list 过程只有在加根结点时才会改变 result-list ,而根结点会被加在第一个位置,所以可以肯定,左子树的位置是在最前面,因此,第二个过程的生成的表顺序也是左子树、根、右子树,和第一个过程一样。
b) 其实在我看来,因为两者都要遍历所有的结点,都需要n步,所以两者的消耗是一样的。。但既然书上这么问了,那肯定是不一样的。。鉴于算法分析一直是我弱项,所以我果断去Google了一下,发现了这个解答。他讲得挺清楚了,我就简单复述一下:因为第一个过程用到了 append ,而 append 的步数依赖于第一个参数的长度,这个参数恰好是左子树,对于平衡二叉树来讲,每次都访问某个子树的步数是O(log n),所以,第一个过程的步数是O(n * log n);第二个过程,因为每次递归只调用到了一个常量级别的 cons ,所以它的步数就是O(n)。(吐槽:其实我想对了,不过只想对了一半,谁能想道竟然还要去分析它们子调用的复杂度。。)
练习2.64
a) partial-tree 这个函数很精妙,尤其是返回值,为了方便递归调用,将返回值定义成了两部分: car 是真正的转换后的平衡树, cdr 是表中剩下的元素。这样一来,在递归调用时,就很方便地可以取到表中剩下的元素进行操作。过程首先求值了左子树,为了保持树平衡,左子树的元素个数为 (n - 1) / 2 再向下取整,然后,将剩下的元素的首元素作为树的根结点,再利用再次剩下的元素求值右子树,右子树的元素个数为 n - 左子树元素数 - 1 。
b) 因为要从列表中构建n个元素的树,必须访问这n个元素,所以复杂度就是O(n),但鉴于上一个练习,所以这次学乖了,还要看看 partial-tree 里面有没有子调用是消耗比较大的,但实际上只有一个常量级的 cons 操作,所以整个步数量级就是O(n)。
练习2.65
偷懒的办法:先利用 tree->list 将树转换成有序表,再利用前面已经定义过的对有序表求交并集的过程得到结果,最后再利用 list->tree 给转换回来。。
(define (union-set set1 set2)
(define (list-union-set set1 set2)
(cond ((null? set1) set2)
((null? set2) set1)
(else
(let ((x1 (car set1))
(x2 (car set2)))
(cond ((= x1 x2) (cons x1
(list-union-set (cdr set1)
(cdr set2))))
((< x1 x2) (cons x1
(list-union-set (cdr set1)
set2)))
((> x1 x2) (cons x2
(list-union-set set1
(cdr set2)))))))))
(list->tree (list-union-set (tree->list set1)
(tree->list set2))))
(define (intersection-set set1 set2)
(define (list-intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
(else
(let ((x1 (car set1))
(x2 (car set2)))
(cond ((= x1 x2) (cons x1
(list-intersection-set (cdr set1)
(cdr set2))))
((< x1 x2) (list-intersection-set (cdr set1) set2))
((> x1 x2) (list-intersection-set set1
(cdr set2))))))))
(list->tree (list-intersection-set (tree->list set1)
(tree->list set2))))
练习2.66
(define (lookup given-key tree-of-records)
(cond ((null? tree-of-records) #f)
((= (key (entry tree-of-records)) given-key) (entry tree-of-records))
((> (key (entry tree-of-records)) given-key) (lookup (left-branch tree-of-records)))
(else (lookup (right-branch tree-of-records)))))
练习2.67
这个题目的目的,就是让我们把所有的代码都敲一遍。。
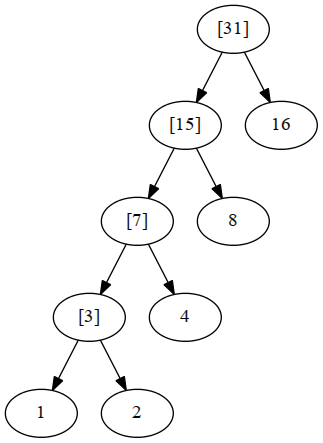
最后结果: (A D A B B C A)
练习2.68
(define (symbol-on-tree? symbol tree)
(memq symbol (symbols tree)))
(define (encode-symbol symbol tree)
(cond ((not (symbol-on-tree? symbol tree))
(error "symbol is not on this tree"))
((leaf? tree) '())
(else (let ((left (left-branch tree))
(right (right-branch tree)))
(if (symbol-on-tree? symbol left)
(cons 0 (encode-symbol symbol left))
(cons 1 (encode-symbol symbol right)))))))
练习2.69
其实这个题目我觉得并不难,不知道为什么出题者在题目后面缀了那么大一段说明。。
(define (successive-merge leaf-set)
(if (= (length leaf-set) 1)
(car leaf-set)
(successive-merge (adjoin-set (make-code-tree (cadr leaf-set)
(car leaf-set))
(cdr (cdr leaf-set))))))
练习2.70
encode消息的相关变量定义及调用:
(define symbol-frequency-pairs
'((A 2) (NA 16)
(BOOM 1) (SHA 3)
(GET 2) (YIP 9)
(JOB 2) (WAH 1)))
(define huffman-tree (generate-huffman-tree symbol-frequency-pairs))
(encode '(GET A JOB
SHA NA NA NA NA NA NA NA NA
GET A JOB
SHA NA NA NA NA NA NA NA NA
WAH YIP YIP YIP YIP YIP YIP YIP YIP YIP
SHA BOOM) huffman-tree)
由Huffman编码后的二进制位个数为84。
如果不用Huffman编码而使用定长编码的话,所有的符号共有15个字母,也就是需要4位来表示一个字母,而这些符号总共有89个字母,所以定长编码需要的二进制位个数为 89 * 4 = 356。这一长度是使用Huffman编码长度的四倍还多了20个二进制位。
练习2.71
对于这样权重组成的符号,因为 2 ^ (n - 1) + 2 ^ n < 2 ^ (n + 1) , 2 ^ (n - 1) + 2 ^ n + 2 ^ (n + 1) < 2 ^ (n + 2) ,所以,构造Huffman树的话,每一步构造出来的树的权重都是最小的,因此,具有最高权重的符号必然只需要一个二进制位,而最不频繁的符号,则需要 n - 1 个二进制位。
n = 5对应的Huffman树如下图所示: